Skip to contents

Regression Diagnostic Plots with ggplot2

Source: R/gg_lm.R
gg_lm.Rd

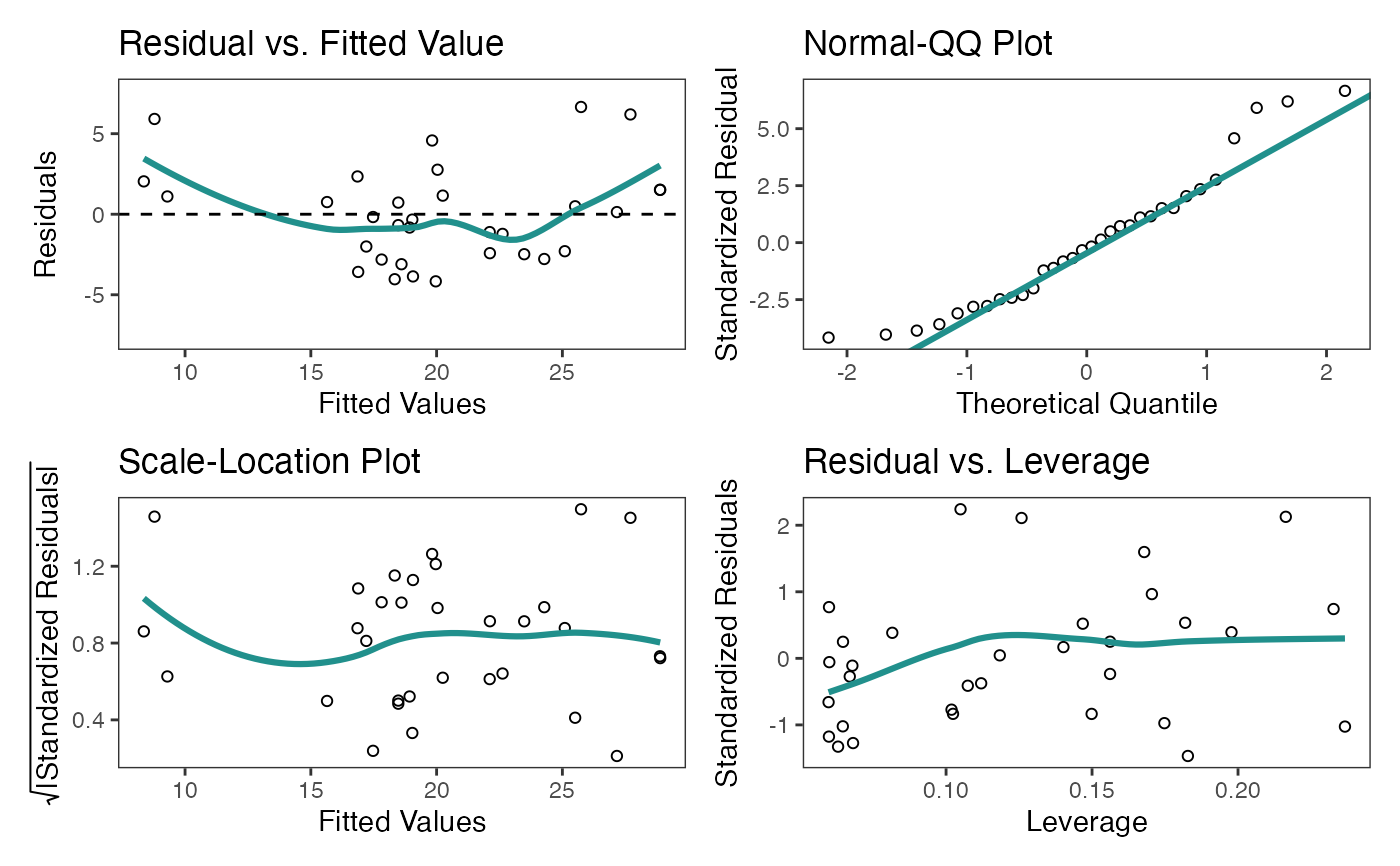
Regression Diagnostic Plots with ggplot2

Usage

gg_lm(
  model,
  which_plots = 1:4,
  cooksD_type = 1,
  standard_errors = FALSE,
  point_size = 1.5,
  theme_color = "#21908CFF",
  n_columns = 2
)

Arguments

model

Model of class "lm" or "glm"

which_plots

Choose which diagnostic plots to choose from.
Options are 1 = 'residual vs fitted', 2 = 'Normal-QQ', 3 = 'Scale-location', 4 = 'Residual vs Leverage', 5 = "Cook's Distance". 6 = "Collinearity". Default is 1:4

cooksD_type

An integer between 1 and 4 indicating the threshold to be computed for Cook's Distance plot. Default is 1. See details for threshold computation

standard_errors

Display confidence interval around geom_smooth, FALSE by default

point_size

Change size of points in plots

theme_color

Change color of the geom_smooth line and text labels for the respective diagnostic plot

n_columns

number of columns for grid layout. Default is 2

Value

Regression diagnostic plots

Details

Plot 5: "Cook's Distance": A data point having a large Cook's distance indicates that the data point strongly influences the fitted values of the model. The default threshold used for detecting or classifying observations as outers is \(4/n\) (i.e cooksD_type=1) where \(n\) is the number of observations. The thresholds computed are as follows:

  • cooksD_type = 1: 4/n

  • cooksD_type = 2: 4/(n-p-1)

  • cooksD_type = 3: 1/(n-p-1)

  • cooksD_type = 4: 3* mean(cook's distance values)

where \(n\) is the number of observations and \(p\) is the number of predictors.

Plot 6: "Collinearity": Conisders the variance inflation factor (VIF) for multicollinearity:
Tolerance = \(1 - R_j^2\), VIF = (1/Tolerance) where \(R_j^2\) is the coefficient of determination of a regression of predictor \(j\) on all the other predictors. A general rule of thumb is that VIFs exceeding 4 warrant further investigation, while VIFs exceeding 10 indicates a multicollinearity problem

References

Belsley, D. A., Kuh, E., and Welsch, R. E. (1980). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New York: John Wiley & Sons.

Sheather, S. (2009). A modern approach to regression with R. Springer Science & Business Media.

Examples

model <- lm(mpg ~ wt + am + gear, data = mtcars)
gg_lm(model)